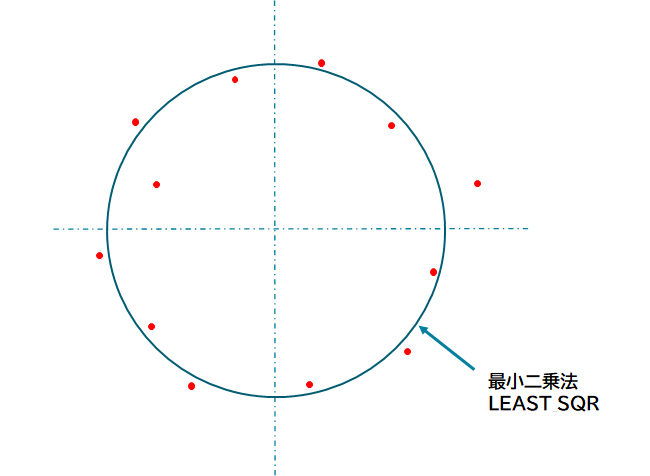
境界(筆界)復元の基本は確率論と最小二乗法の二つです つまり,較差は正規分布になっている 較差の二乗和が最小となる座標値が最適な値である この計算を座標値,基になる図面の座標値(旧座標とここでは言います)と現存二乗和を最小化する方法であるが、 最小化する前に人為的に設定した対象物の方向が、直線の方向 とほぼ平行であるので、"最小二乗法"の適用結果と ほぼ同一の結果が得られる。 なお、最小二乗法は、当てはめようとする直線に対する縦軸方向の偏差のべるが最小領域法と密接なかかわりがある また,実 際の測定では,雑 音・バリ・ごみ等の異常デー タが混入する場合がありうるので,こ れを取り除く必要が 出てくる 2 1 最小二乗法による形状の決定 最小二乗法を用いて形状を求める場合,主 たる考え方は
最小二乗法 Least Squares Method
公差設定 最小二乗法
公差設定 最小二乗法-最小二乗法は、この「最小二乗の条件」を使って、 解を推定する計算手法である。 これにより、観測値はばらつき(誤差を持ち)、 たくさんの余剰な観測があるため、解がひとつ に決まらないという状態(解不定)から脱するこ とができるのである。幾何公差 6.-2/6 幾何公差q&a 9.回転体でないのに円周振れの公差があります、これって使い方間違っていませんか。 データム軸直線を軸とする回転面及び円形平面があればいいと思います。 10.データム平面と平面度の違いを教えて下さい。



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
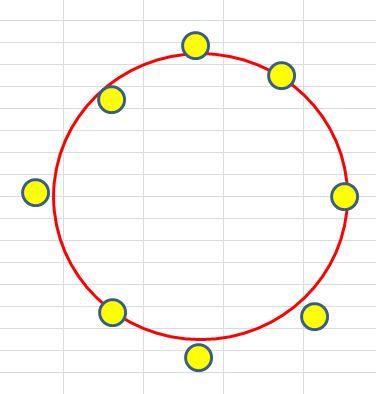
二乗和平方根(Root Sum Squire) 起こり得る可能性の少ない公差の最大・最小領域の寸法を含めずに、それぞれの公差を二乗して積み上げ、平方根で返すことで得られるバラツキの予測値です。 ワーストケースと二乗和平方根、どちらの方法を計算として適用①最小二乗法 ②外接法 ③内接法 ※ 測定する円を黒で表示 測定した値を赤で表示 誤差の二乗の和が最小にな る円を求めるため、数値は 外接円と内接円の中間に近 い数値になります。 内接円を求めるため、 数値は小さくなります。 外接円を求めるため、 最小二乗法(LSMLeast Squares Method)などに使用する統計量となっており、残差(実値と推定値との差分)を二乗(平方)して足したものとなります。 誤差二乗和 とも呼ばれます。
1 最小二乗法(1) 同じ対象に対する同じ計測 ⇒同じ誤差をもつ計測 このときには平均値が最尤推定量となる では同じ量を2つの方法で計測したら? ⇒一般にはそれぞれの計測誤差は異なる統計的に正しいけど累積公差計算 (二乗和平方根)の基本と限界 部品は図面やデータから実体を持ったとき、必ずデータ上の形状からブレが生じます。 同じ部品を複数作ったとしたら、このブレは均一ではなく、場所や程度にバラツキも生じます。 なの2.2.二乗和の根拠(誤差伝播の証明) 前節で個々の部品の公差を\( \sigma \)管理としたとき、二乗和による累積公差も\( \sigma \)管理となること、その理由は誤差伝播の法則に従うため、と述べました。そこで、本項では二乗和の根拠となる"誤差伝播の法則"について見ていきます。
この記事ではこんなことを書いています 最小二乗法によってデータの回帰直線を求める方法を丁寧に解説していきます。 まずは、最小二乗法とは何かということを数式を使わずにざっくりと理解します。 その後、最小二乗法の式の導出を途中の計算式を省略せずに紹介します。 最後に、LSC最小二乗中心法 MZC最小領域中心法 MCC最小外接円中心法 MIC最大内接円中心法 R m a x R mi Δ Z q R m a x R mi n Δ Z c m x R mi n Δ z R m a x mi n Δ Z i フィルタのカットオフ値の違いによる真円度の値の差 フィルタのカットオフ値が異なると真円度値にも大きく影響する6.寸法と寸法公差の記入法 Φ50 Φ 0015 50:基準寸法 Φ:直径 0015 Φ50 0 0035 Φ 0 Φ50±0025 公差の上限 公差の下限 寸法 図面において、寸法値と公差値の単位はmmであり、 単位を図面に記入する必要がない。



寸法公差 機械製図



さまざまな幾何公差 その1 その定義や例 測定方法について 産機設計者が解説 公差計算 公差解析 6 3 3 ページ Monoist
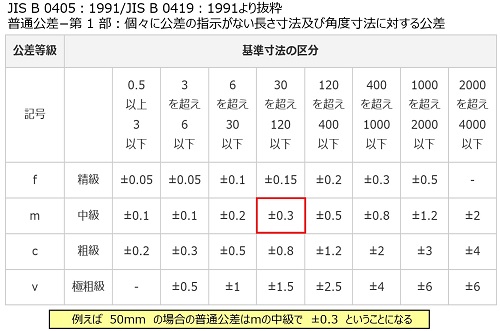
第5回目のお題は『公差計算』についてです。これも機械設計をやっていくで必ず必要になる知識ですので、今回の題材にすることにしました。公差の積み上げ計算方法については、大きく2種類あります。 1つ目は「PP法」というもので、peak to peak(ピークトゥーピーク)の略で、公差最小2乗法は上述の1次式だけでなく,さまざまな形式の回帰式に適用することができる。 \(n\) 組のデータ \( (x_i\ y_i ) \) を回帰式 \(y=ax \) に近似する方法を説明せよ。 解法1および解法3について,それぞれ解いてみよう。 解法3では,「オプション」タブのISO178と JIS K7171 5 項目 JIS K7171 ISO 178 推奨 試験片 厚さ 4mm±02mm 4mm±02mm 幅 10mm 10mm 試験力精度 JIS B 7721 1級(±1%) (=ISO Class 1(±1%))



円の最小二乗法 とりどんの言いたい放題



公差設計
いままで, 最小二乗法は最も一般的な方法とはいえ, 余りにも無批判に用いられてきたきらいがある 従来の 最小二乗法については, 解法以前に検討すべき点も多 い 各成分に同程度の誤差が含まれていると考える本論 の方法は計算も非常に簡単である公差と間違わないようにするために"かくさ"ということもあります。較差とは最高と最低、最大 と最小の差です、測量では2個の観測値の差。 現存している境界標等の図面成果を実測成果に重ねます,最小二乗法という方法を使いま平均二乗誤差の3倍は公差になっていますので,公差の 3×√2=424分の1が標準偏差と なります。これは確率分の9999に相当します。 このことから,国土調査法施行令別表4 にある距離の公差,面積の公差も分の
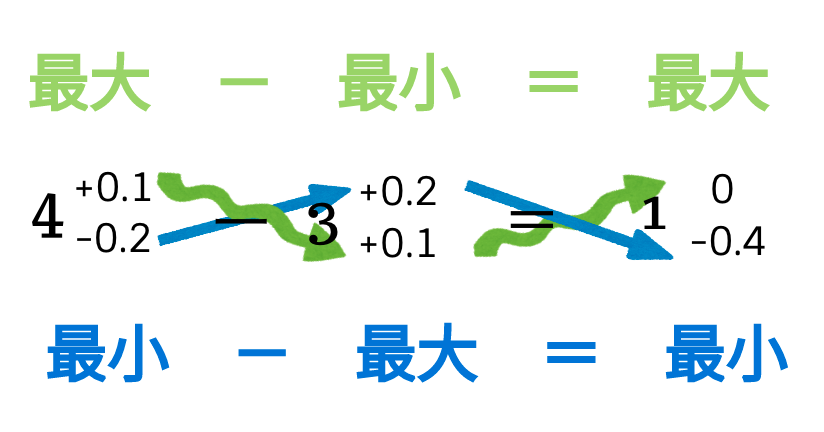



公差解析01 公差の足し算引き算 エクセルや標準偏差sを扱う前に基本を確認 機械設計者の皆様 教わらなかったことは常識だそうです
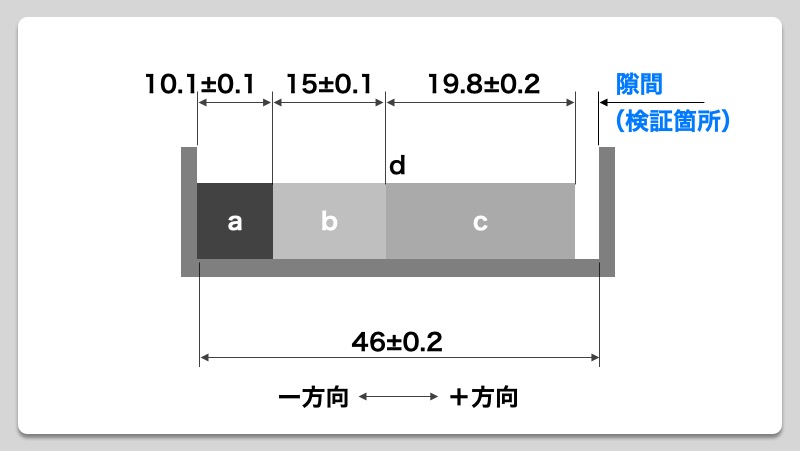



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
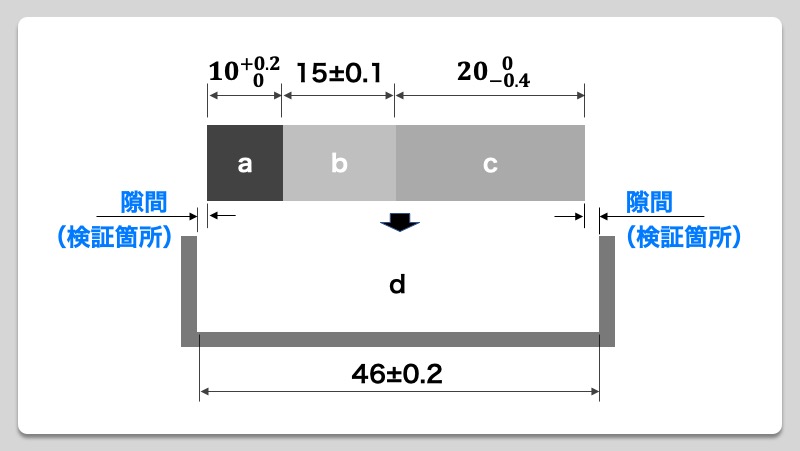
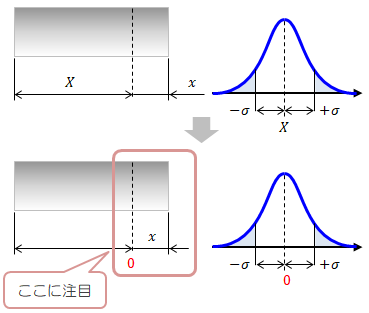
狙い目を寸法数値に置き換え上公差、下公差を有する公差にしてから二乗法を導入して計算する方法。 よって公差は±016となり aは6±016→aは616~584の段差を有する。 この結果、図面寸法法と中間値法では、ほぼ同じ値がでました。最小二乗法(さいしょうにじょうほう、さいしょうじじょうほう;最小自乗法とも書く、英 least squares method )は、測定で得られた数値の組を、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残公差計算を行う際、計算結果の値が正規分布の "3σ:997%" の範囲内となるよう各公差を2乗和平方根を用いた累積計算を行います。この2乗和平方根による公差計算ですが、過去に私が統計学の正規分布を少しかじり始めた頃、"3σ:997%" ではなく "標準偏差σ:6%" の部分を計算している
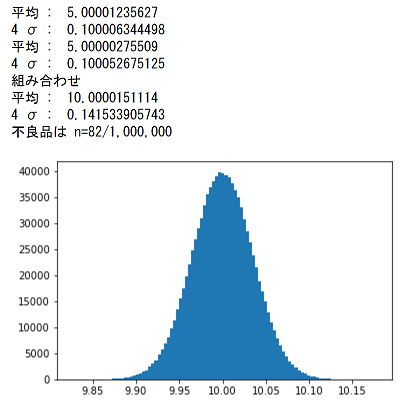



二乗和平方根とモンテカルロ法を比べてみた



5 累積公差とは 株式会社 ケープヒル コンテムズ
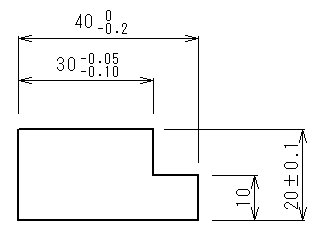
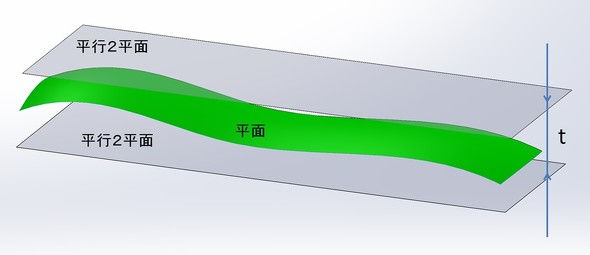
基準円の種類 最小二乗基準円(LSC) 最小二乗基準円は、この円の内側の面積の合計が円の外側の面積の合計に等しく、最小間隔に保たれている円です。 真円度からの偏位は、基準円の中心からの半径方向の偏位の最大値と最小値の差です。 これは数学5 寸法公差の妥当性を検証する 前回までに、寸法公差の記入法や使い方、面の肌記号の意味と記入上の注意点について学習した。 最終回は、寸法公差を図面に記入する際に公差値の妥当性を検証する考え方を解説する。 一部品内の公差の検討1章 幾何公差方式の基本 113 円筒形体の横断面と中心線 軸の円筒面(円筒面上の座標値の集合であってもよい)が、図13に示すよ うに曲がって測定されたとする。実測した円筒面に対して、最小二乗




最小二乗法 人事のための課題解決サイト Jin Jour ジンジュール




08 号 公差決定方法 公差決定装置 プログラム および記録媒体 Astamuse
規定された幾何公差検証手順に則った計測点群に対する平面, 円筒面等の形体フィッティング,及び幾何公差の評価が不可欠 である.しかし,最小二乗法による形体フィッティングは,レ ーザスキャナのような比較的高密度だが確度が中程度の計測



最小二乗法とか メモ帳 Fmaj7b5 Info
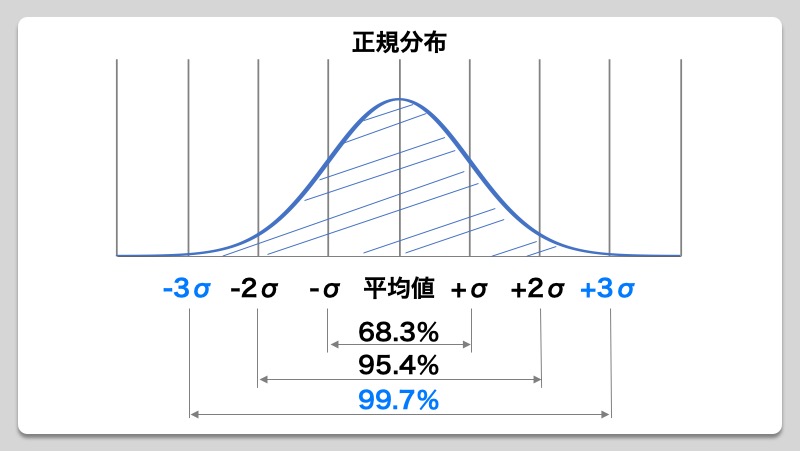



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
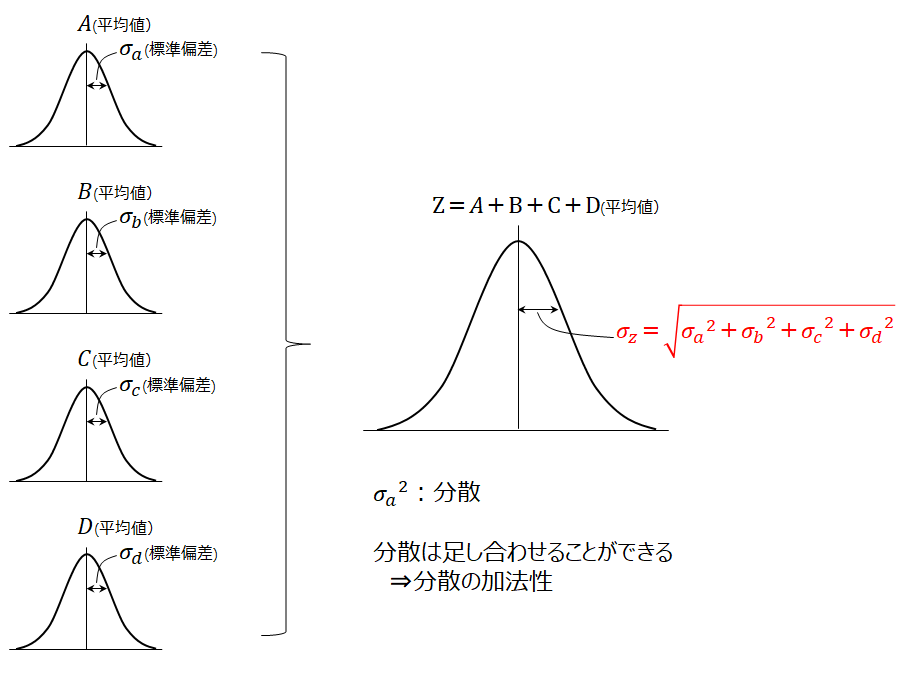



累積公差の計算 二乗和平方根 製品設計知識
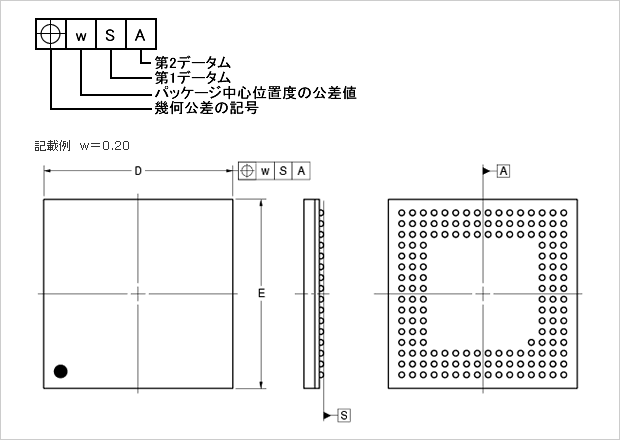



パッケージ中心位置度 W Renesas



5 累積公差とは 株式会社 ケープヒル コンテムズ



2
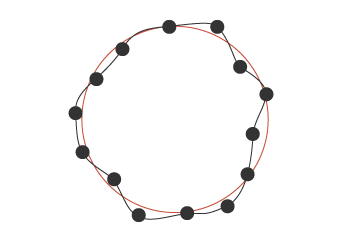



測定機 幾何公差を測定する機器と原理 ゼロからわかる幾何公差 キーエンス



平均二乗誤差



ケーススタディで理解する幾何公差入門 幾何公差 図面 製図 機械設計 機械 本 雑誌 日刊工業新聞




公差分析編 ライブラリ Opeo 折川技術士事務所
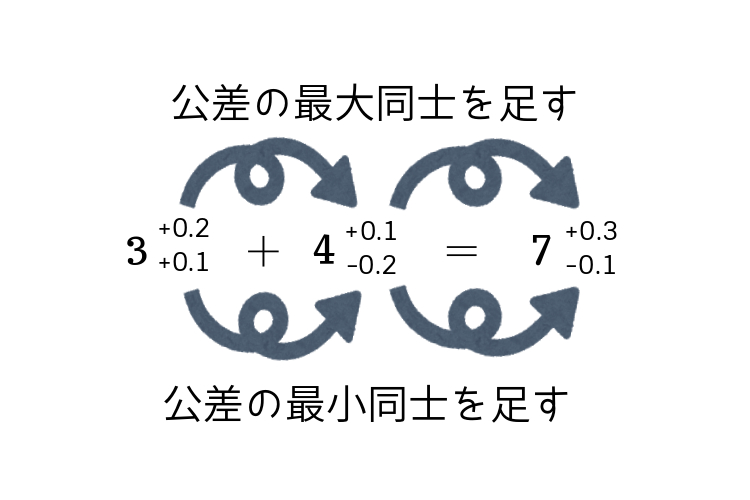



公差解析01 公差の足し算引き算 エクセルや標準偏差sを扱う前に基本を確認 機械設計者の皆様 教わらなかったことは常識だそうです
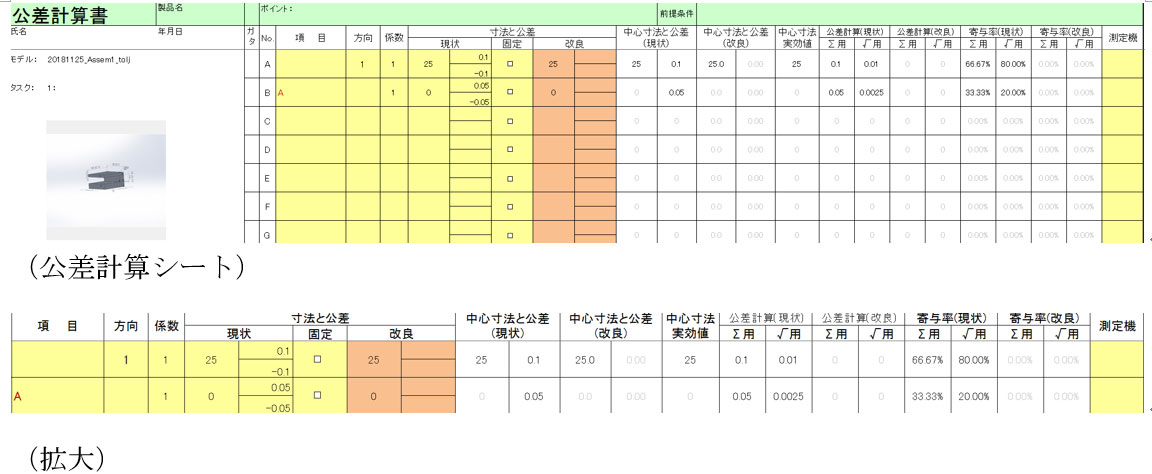



独立の原則を頭に入れて測定したり アセンブリーを設計したりする 3d設計推進者の眼 35 1 5 ページ Monoist




製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
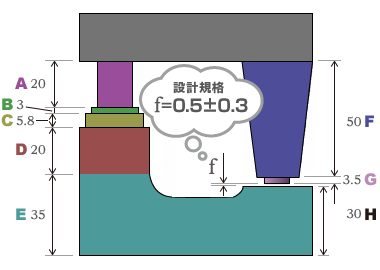



公差設計のメリット 計算事例 公差設計1 技術情報 Misumi Vona ミスミ




機械加工部品のエッジ品質及びその等級 jisによらない機械製図
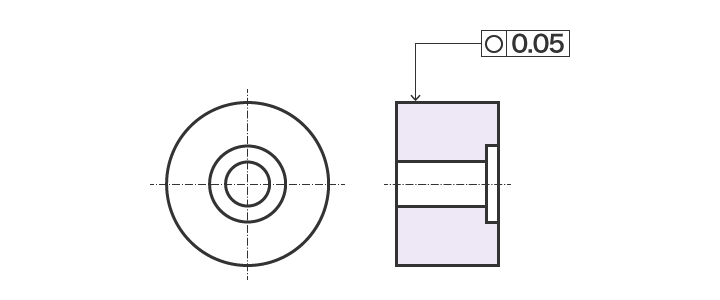



真円度の測定 形状公差の測定 ゼロからわかる幾何公差 キーエンス



最小二乗法について



最小二乗法 Least Squares Method



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度




05 機械設計 公差の二乗和平方根をエクセルで計算してみた 基礎知識 好きな事で生きていく
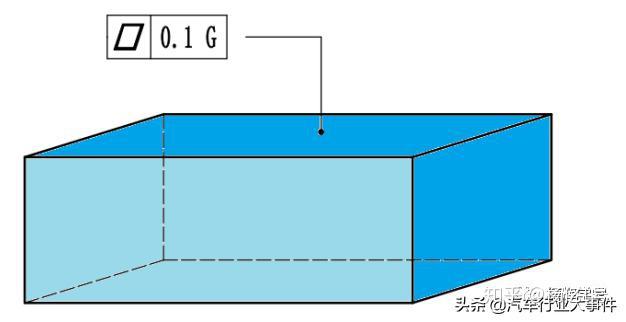



Gd T干货 最小二乘法的数学公式详解 知乎




1996 0519号 中心要素の測定方法および装置と公差測定方法 Astamuse



Pc Dmis デーミス Ncの使える機能 機上計測 計測 工場の自動化ソリューションサイト 株式会社キャプテンインダストリーズ



技術計算製作所 公差の考え方 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Mech Engineer General Tol




最小二乗法とは 公式の導出をわかりやすく高校数学を用いて解説 平方完成の方法アリ 遊ぶ数学
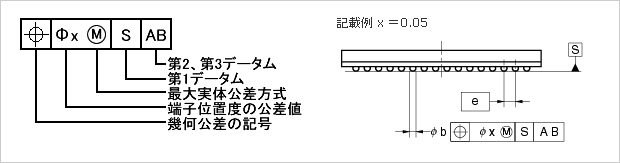



端子位置度 X Renesas



19 Whatsnew Iso 公差付記記号
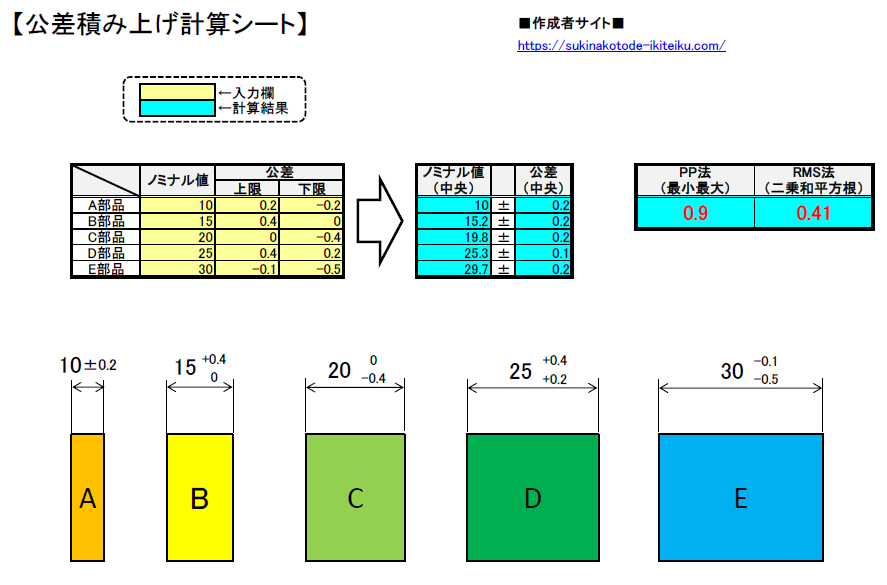



05 機械設計 公差の二乗和平方根をエクセルで計算してみた 基礎知識 好きな事で生きていく




公差に対する思い込み 日経クロステック Xtech



2
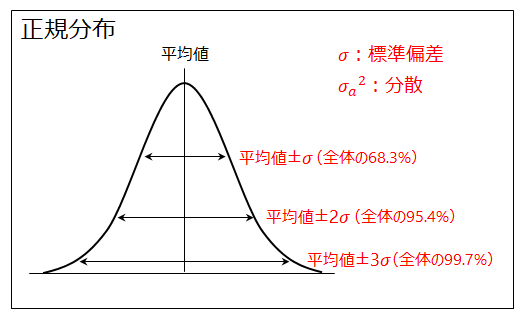



累積公差の計算 二乗和平方根 製品設計知識




08 号 公差決定方法 公差決定装置 プログラム および記録媒体 Astamuse



二乗平均平方根などの統計量について



情報処理実習2
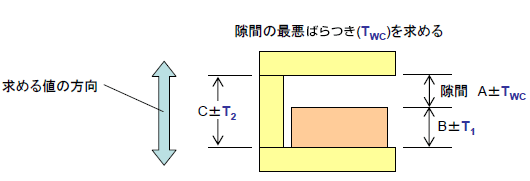



公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット
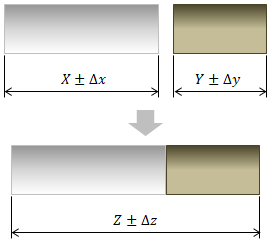



技術計算製作所 公差の考え方 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Mech Engineer General Tol



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度
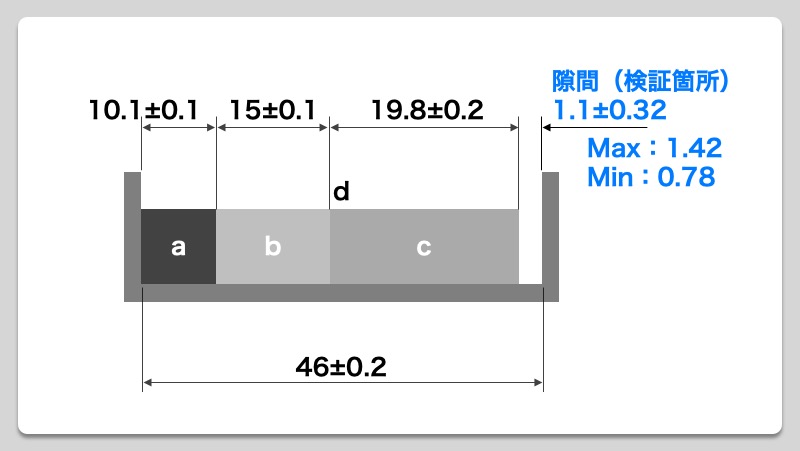



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
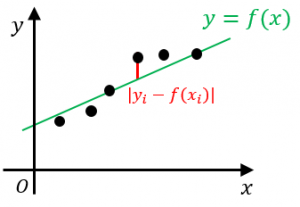



最小二乗法と最尤法の関係 具体例で学ぶ数学




最小二乗法 平均二乗誤差 中学生から分かるai数学 2 1 E資格対応 Youtube



トロイダル面評価方法




機械学習アルゴリズム基礎



平均二乗誤差



標準精密ボールねじ 株 伊和起ゲージ Iwakigauge デジアナeカタログ メカトロネット




08 号 公差決定方法 公差決定装置 プログラム および記録媒体 Astamuse
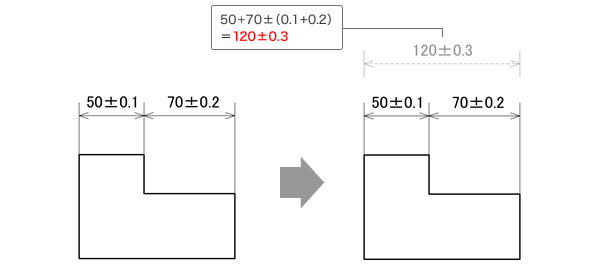



寸法公差の妥当性を検証する 世界で戦えるglobalエンジニアになるための製図技術 4th Step 第5回 お客様マイページ 大塚商会




公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット
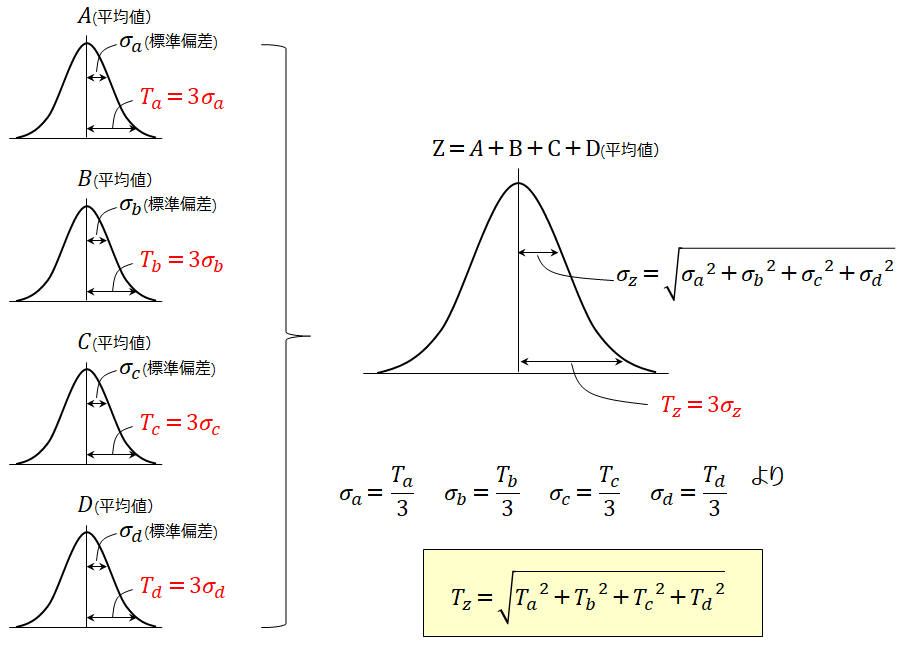



累積公差の計算 二乗和平方根 製品設計知識



2



1
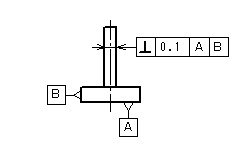



直角度公差 機械製図




統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から



さまざまな幾何公差 その1 その定義や例 測定方法について 産機設計者が解説 公差計算 公差解析 6 3 3 ページ Monoist



分散公式




要因数と累積誤差 ライブラリ Opeo 折川技術士事務所



二乗平均平方根などの統計量について



最小二乗法を使わない簡単な直線回帰のやりかた



テクニカルレポート Busicom Post
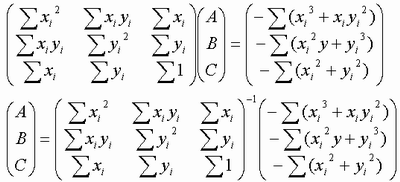



一般式による最小二乗法 円の最小二乗法 イメージングソリューション




測定工具の使い方 2 使用方法 メイン 2 11 3次元測定機の穴径比較



2




幾何公差 メイン 6 2 6 幾何公差q A



原始筆界
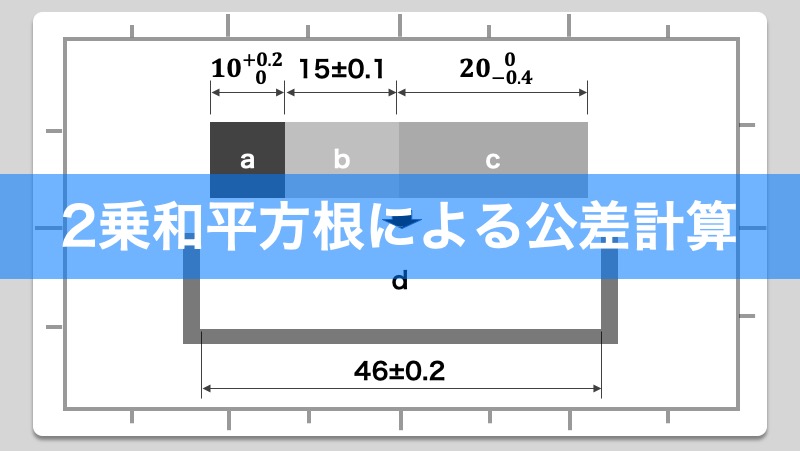



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes




幾何公差 メイン 6 2 6 幾何公差q A




統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から
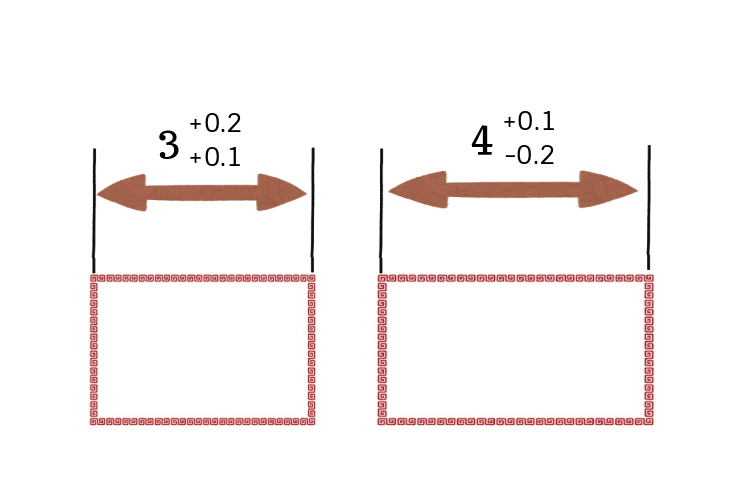



公差解析01 公差の足し算引き算 エクセルや標準偏差sを扱う前に基本を確認 機械設計者の皆様 教わらなかったことは常識だそうです
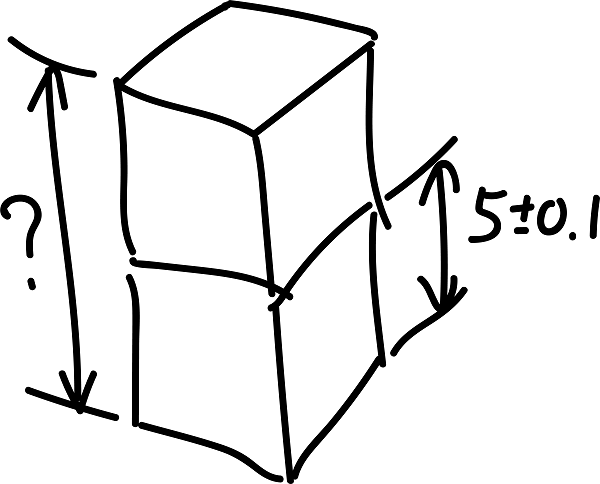



二乗和平方根とモンテカルロ法を比べてみた




最小二乗法 Wikipedia
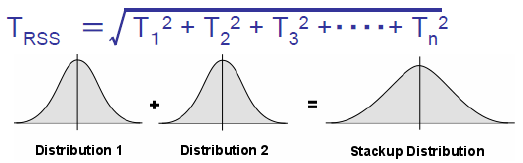



公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット



Excelでの最小二乗法の計算
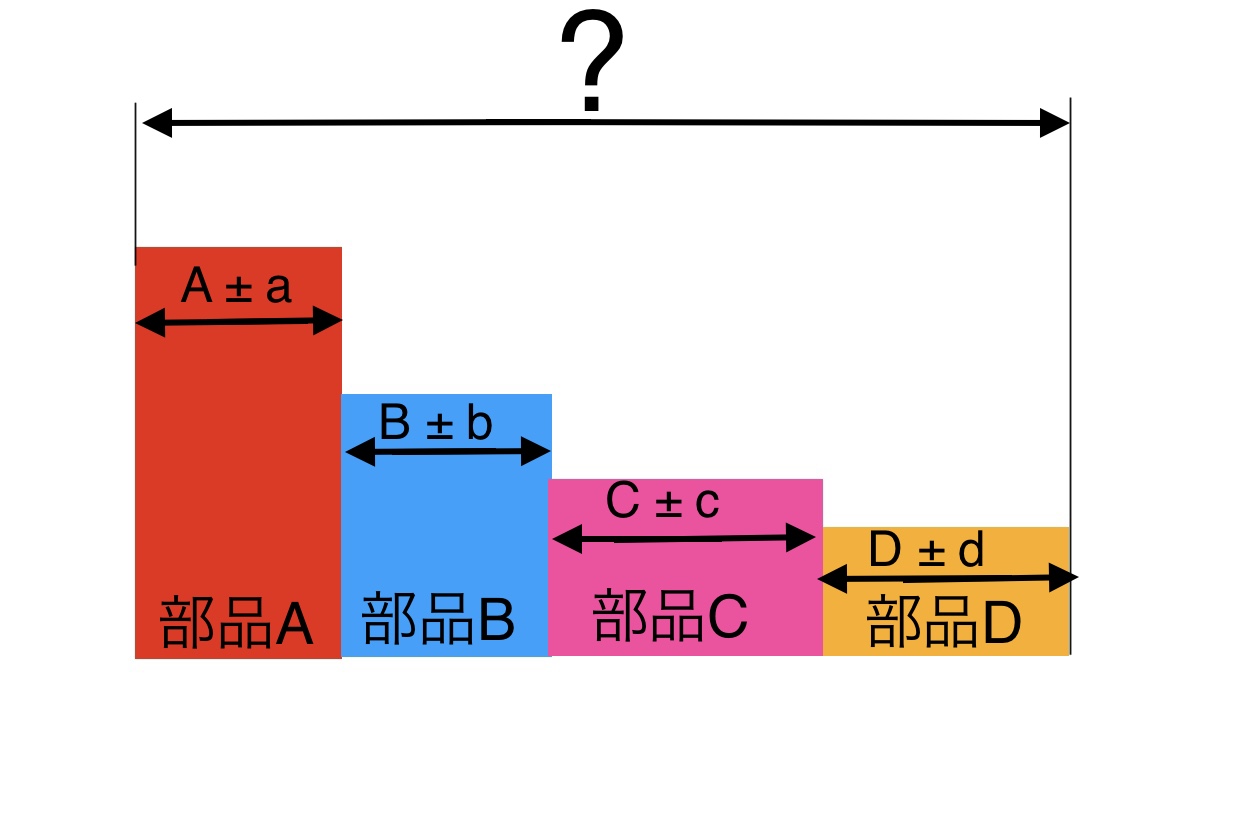



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度




統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から




非線形最小二乗法 Wikipedia



最小二乗法 簡単すぎて かえって難しい
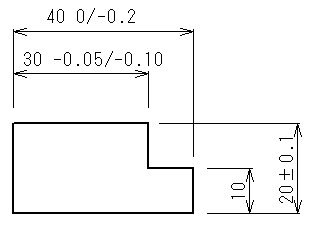



寸法公差 機械製図
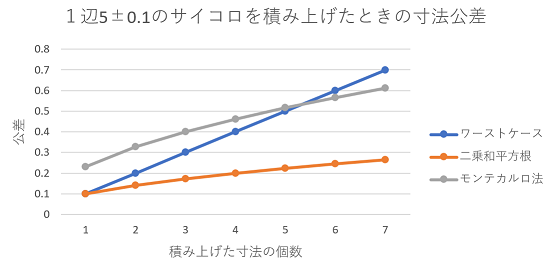



二乗和平方根とモンテカルロ法を比べてみた




データム形体と実用データム形体 ライブラリ Opeo 折川技術士事務所




最小二乗法の意味と計算方法 回帰直線の求め方




太陽パーツ テクニカルニュース Vol 17 ブログ 太陽パーツ株式会社 機械部品 住設機器の設計 製造



工程能力と公差解析 理論編と実践編



1
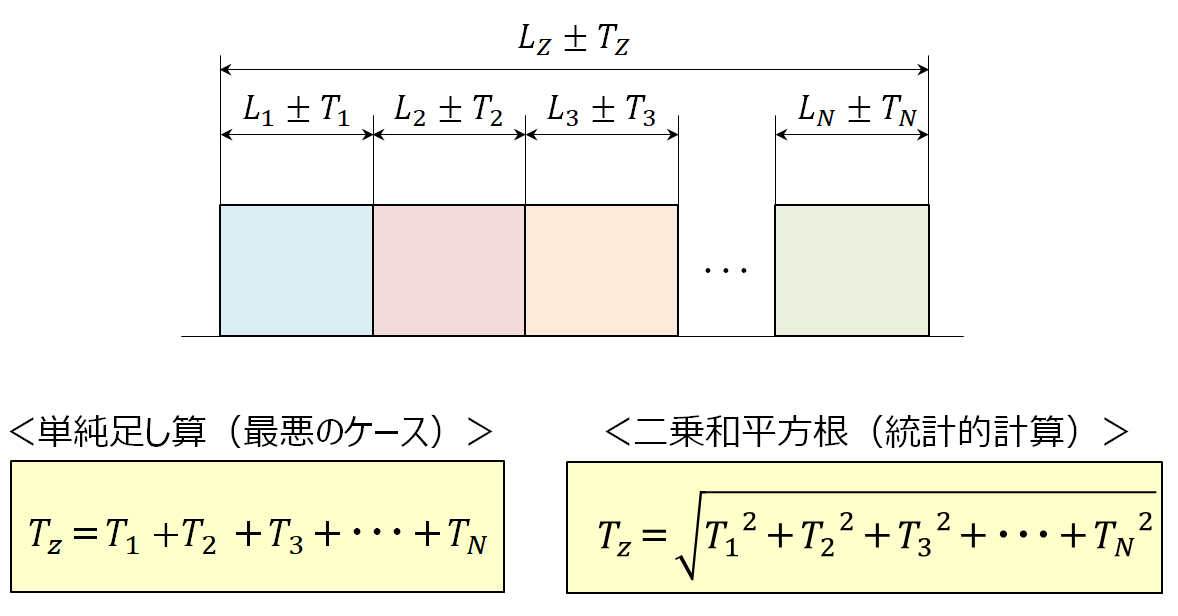



累積公差の計算 二乗和平方根 製品設計知識
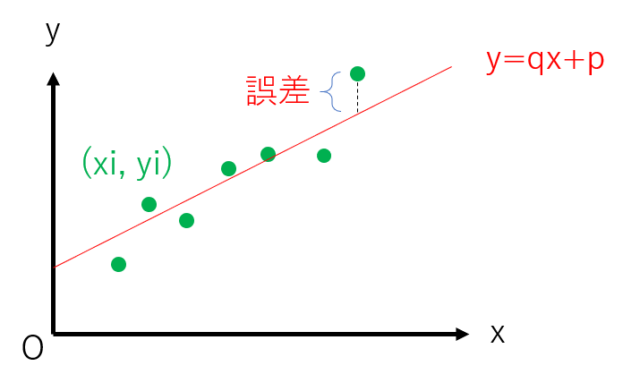



行列の最小二乗法について調べてみた Developersio



最小二乗法について



グローバル図面 新iso準拠 って どない描くねん 製図 図面 機械設計 幾何公差 機械 本 雑誌 日刊工業新聞



二乗平均平方根などの統計量について



3
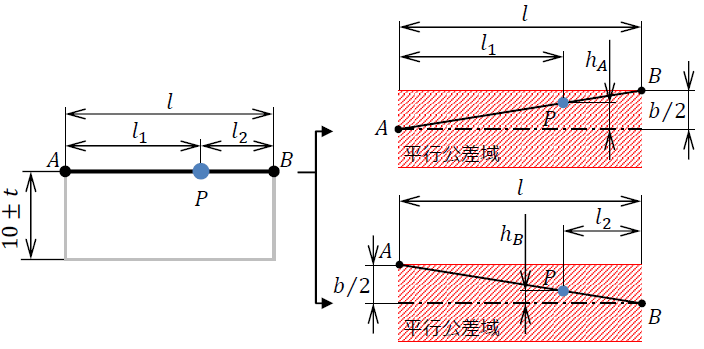



公差分析編 ライブラリ Opeo 折川技術士事務所
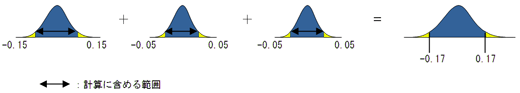



ワーストケースと二乗和平方根って 何 公差解析 基本中の基本 2 4 4 ページ Monoist



5 累積公差とは 株式会社 ケープヒル コンテムズ




最小二乗法の式の導出と例題 最小二乗法と回帰直線を思い通りに使えるようになろう 数学の面白いこと 役に立つことをまとめたサイト



公差設計




製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes



No comments:
Post a Comment